예를 한번 보면 도움이 되겠지요..
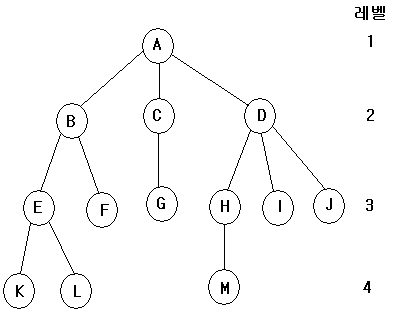
노드의 갯수 : 13개
A의 차수 : 3
B의 차수 : 2
F의 차수 : 0
트리의 차수 : 3
단말노드(leaf or terminal node) : K, L, F, G, M, I, J
B는 E와 F의 부모.
H, I, J는 형제
M의 조상 : A, D, H
B의 자손 : E, F, K, L
트리의 깊이 : 4
트리의 표현
리스트 표현 : (A (B (E (K,L), F), C(G), D(H (M), I, J)))
왼쪽자식-오른쪽형제 표현(left child-right sibling)
왼쪽자식-오른쪽자식 표현
: 왼쪽자식-오른쪽형제 표현을 시계방향으로 45도 회전.
※ 모든 트리는 이진트리로 변경할 수 있다.
트리용어에대한 간략한 내용 입니다.
트리
- 정의 : 1개 이상의 노드(node)로 이루어진 유한집합.
(1) 노드 중에는 근 노드(Root node)가 하나 존재한다.
(2) 나머지 노드들은 n>=0개의 분리집합 T1,…Tn으로 분리가 가능하다.
노드(Node )
: 데이타와 이것으로부터 다른 노드로 뻗어진 가지를 함께 부른다.
차수(Degree)
: 노드의 서브 트리 수
트리의 차수
: 해당 트리에 있는 노드 중 최대 차수를 갖는 노드의 차수
단말노드(terminal node or leaf)
: 차수가 0인 트리
부모(Parent)
: 서브 트리를 갖는 노드.
자식(Children)
: 부모노드 아래의 서브 트리의 Root 노드
형제(sibling)
: 같은 부모(Parent)를 갖는 node들
조상(ancestors)
: 루트에서 해당 노드의 경로상에 존재하는 모든 노드
후손(descendants)
: 한 노드의 서브 트리에 속한 모든 노드
레벨(Level)
: 루트의 레벨(Level)을 1로 가정
트리의 높이 또는 깊이(Height or Depth)
: 해당 트리에 속한 노드의 최대 레벨(Level)
[c] 이진트리(binary tree)의 특성
