[c] 이진트리(binary tree)의 특성

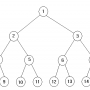
이진트리의 특성입니다.

- 모든 노드들의 차수가 2이하.

- 왼쪽 서브트리와 오른쪽 서브트리를 구별한다.(일반트리 - 구별없음)

- 0개의 노드를 가질 수 있다(공집합). 

※정의: 이진트리는 공집합이거나 루트와 왼쪽서브트리,오른쪽 서브트리

       라고 부르는 두 개의 분리된 이진트리로 구성된 노드의 유한집합.

- 이진트리의 레벨 i에서의 최대 노드 수는 2의(i-1)승 (i>=1)이다.

- 깊이가 k인 이진트리가 가질 수 있는 최대 노드수는 2의 k승 -1(k>=0).

- 단말노드의 수 = 차수가 2인 노드수 + 1

※포화이진트리(full binary tree)

- 깊이가 k이고 최대 노드수를 갖는 이진트리

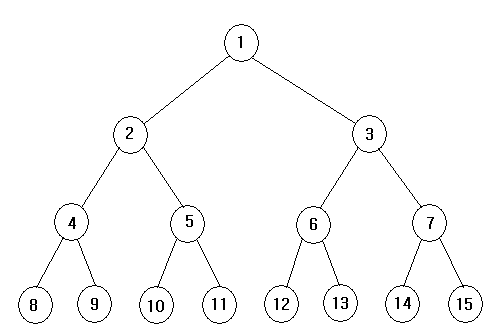
※완전이진트리(complete binary tree)

- 깊이가 k이고 노드수가 n인 이진트리가 만일 이 트리의 각 노드들이

  깊이 k인 포화이진트리에서 1부터 n까지 번호를 붙인 노드들과 일대일

  로 일치하면 이트리는 완전이진트리이다.

완전 이진트리가 깊이와 순서에 따라 표현되어 있을 때 인덱스

i (1<= i <=n)인 모든 노드에 대하여 다음 정보를 얻을 수 있다.

1) i != 1 이면 i의 부모노드는 i/2의 위치에 있게된다.

2) 2i <= n 이면 i의 왼쪽 자식은 2i의 위치에 있게된다.

    만일, 2i > n 이면 i는 왼쪽 자식을 가질 수 없다.

3) 2i+1 <= n 이면 i의 오른쪽 자식은 2i+1의 위치에 있게된다.

    만일, 2i+1 > n 이면 i는 오른쪽 자식을 가질 수 없다.