[c] 이진트리/트리 순회법 코드(전위/중위/후위)

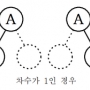
이진트리(BinaryTree)
- 일반적인 트리는 한 노드가 N개의 자식을 가질 수 있지만 이진트리의 경우 한 노드가 최대 2개의 자식만 가질 수 있다.
- 다양한 분야에 활용되는 자료구조이다. 수식을 트리 형태로 표현하여 계산하게 하는 수식 이진 트리(Expression Binary Tree),
아주 빠른 데이터 검색을 가능케 하는 이진 탐색 트리(Binary Search Tree) 등등.
- 이진트리의 종류 : 포화 이진 트리(Full Binary Tree), 완전 이진 트리(Complete Binary Tree),
높이 균형 트리(Height Balanced Tree), 완전 높이 균형 트리(Completely Height Balanced Tree)

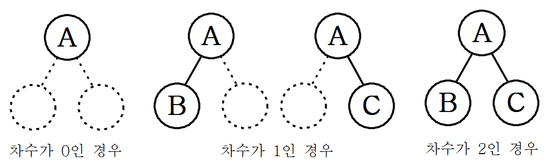
포화 이진 트리(Full Binary Tree)
- 모든 레벨의 노드가 꽉 차있는 이진 트리.
- 단말 노드를 제외한 모든 노드의 차수가 2인 형태를 말한다.

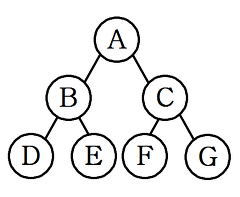
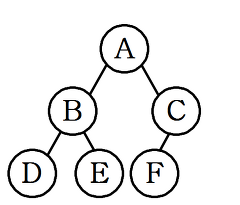
완전 이진 트리(Complete Binary Tree)
- 단말 노드들이 트리의 왼쪽부터 차곡차곡 채워진 형태.
- 무조건 왼쪽부터 채워져 있어야 한다.(왼쪽 하위 트리 중 하나라도 비워져있다면 해당 안됨)

트리 순회법
- 트리 순회 방법에는 3가지가 있다.
- 전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal)

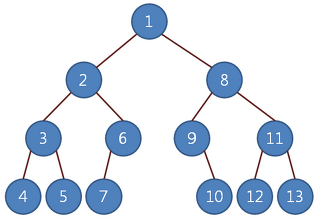
전위 순회법(Preorder Traversal)
1. 루트 노드부터 시작해서 아래로 내려 오면서
2. 왼쪽 하위 트리를 방문하고 왼쪽 하위 트리의 방문이 끝나면
3. 오른쪽 하위 트리를 방문하는 방식

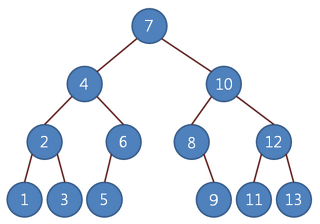
중위 순회법(Inorder Traversal)
- 트리는 하위 트리의 집합이라고 할 수 있고 하위 트리 역시 또 다른 하위 트리의 집합이라고 할 수 있다.
- 따라서 아래와 같은 방법으로 탐색할 수 있다.
1. 왼쪽 하위 트리부터 시작해서
2. 루트를 거쳐
3. 오른쪽 하위 트리를 방문하는 방법

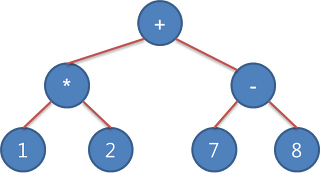
- 응용 사례 : 수식 트리(Expression Tree), 중위 표기식
- (1 * 2) + (7 - 8)을 수식 트리로 표현하면 다음 그림과 같이 나타낼 수 있다.

후위 순회법(Postorder Traversal)
- 전위 순회의 반대
1. 왼쪽 하위 트리부터 시작해서
2. 오른쪽 형제 노드를 방문 후
3. 루트 노드를 방문하는 방법.

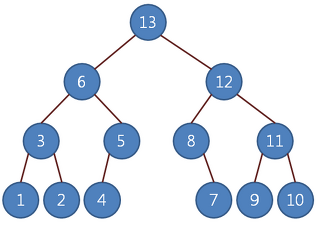
- 응용 사례 : 후위 표기식. 후위 순회법을 통해 출력되는 노드를 살펴보면 후위 표기식으로 나타난다.
- 1 2 * 7 8 - +

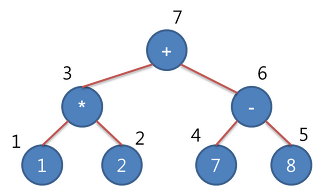
C로 구현한 이진트리/트리 순회법

BinaryTree.h

#ifndef BINARY_TREE_H
 
#define BINARY_TREE_H
 
#include <stdio.h>
#include <stdlib.h>
 
typedef char ElementType;
 
typedef struct tagNode
{
    struct tagNode* left;
    struct tagNode* right;
    ElementType data;
} Node;
 
Node* CreateNode(ElementType newData);
void DestroyNode(Node* node);
void DestroyTree(Node* root);
void PreOrderPrintTree(Node* node);
void InOrderPrintTree(Node* node);
void PostOrderPrintTree(Node* node);
 
#endif

BinaryTree.c

#include "BinaryTree.h"
 
/* 노드 생성 */
Node* CreateNode(ElementType newData)
{
    // 노드를 위한 메모리 할당
    Node* newNode = (Node*) malloc(sizeof(Node));
 
    newNode->left = NULL;
    newNode->right = NULL;
    newNode->data = newData;
 
    return newNode;
}
 
/* 노드 파괴 */
void DestroyNode(Node* node)
{
    free(node);
}
 
/* 트리 파괴(후위 순회 활용) */
void DestroyTree(Node* root)
{
    if(root == NULL)
        return;
 
    // 왼쪽 하위 트리 소멸
    DestroyTree(root->left);
 
    // 오른쪽 하위 트리 소멸
    DestroyTree(root->right);
 
    // 루트 노드 소멸
    DestroyNode(root);
}
 
/* 전위 순회 */
void PreOrderPrintTree(Node* node)
{
    if(node == NULL)
        return;
 
    // 부모 노드 출력
    printf(" %c", node->data);
 
    // 왼쪽 하위 트리 출력
    PreOrderPrintTree(node->left);
 
    // 오른쪽 하위 트리 출력
    PreOrderPrintTree(node->right);
}
 
/* 중위 순회 */
void InOrderPrintTree(Node* node)
{
    if(node == NULL)
        return;
 
    // 왼쪽 하위 트리 출력
    InOrderPrintTree(node->left);
 
    // 부모 노드 출력
    printf(" %c", node->data);
 
    // 오른쪽 하위 트리 출력
    InOrderPrintTree(node->right);
}
 
/* 후위 순회 */
void PostOrderPrintTree(Node* node)
{
    if(node == NULL)
        return;
 
    // 왼쪽 하위 트리 출력
    PostOrderPrintTree(node->left);
 
    // 오른쪽 하위 트리 출력
    PostOrderPrintTree(node->right);
 
    // 부모 노드 출력
    printf(" %c", node->data);
}

Test_BinaryTree.c

#include "BinaryTree.h"
 
void main()
{
    // 노드 생성
    Node* A = CreateNode('A');
    Node* B = CreateNode('B');
    Node* C = CreateNode('C');
    Node* D = CreateNode('D');
    Node* E = CreateNode('E');
    Node* F = CreateNode('F');
    Node* G = CreateNode('G');
 
    // 트리에 노드 추가
    A->left = B;
    B->left = C;
    B->right = D;
 
    A->right = E;
    E->left = F;
    E->right = G;
 
    // 트리 출력
    printf("PreOrder...\n");
    PreOrderPrintTree(A);
    printf("\n\n");
 
    printf("InOrder...\n");
    InOrderPrintTree(A);
    printf("\n\n");
 
    printf("PostOrder...\n");
    PostOrderPrintTree(A);
    printf("\n");
 
    // 소멸
    DestroyTree(A);
}

JAVA로 구현한 이진트리/트리 순회법

Node.java

public class Node {
    private char data;
    private Node left;
    private Node right;
 
    public Node(char data) {
        this.setData(data);
    }
 
    public void setData(char data) {
        this.data = data;
    }
 
    public char getData() {
        return data;
    }
 
    public void setLeft(Node left) {
        this.left = left;
    }
 
    public Node getLeft() {
        return left;
    }
 
    public void setRight(Node right) {
        this.right = right;
    }
 
    public Node getRight() {
        return right;
    }
}

BinaryTree.java

public class BinaryTree {
    // 전위 순회
    public static void preorderPrintTree(Node node) {
        if(node == null)
            return;
         
        // 부모 노드 출력
        System.out.print(" " + node.getData());
         
        // 왼쪽 하위 트리 출력
        preorderPrintTree(node.getLeft());
         
        // 오른쪽 하위 트리 출력
        preorderPrintTree(node.getRight());
    }
     
    // 중위 순회
    public static void inorderPrintTree(Node node) {
        if(node == null)
            return;
         
        // 왼쪽 하위 트리 출력
        inorderPrintTree(node.getLeft());
         
        // 부모 노드 출력
        System.out.print(" " + node.getData());
         
        // 오른쪽 하위 트리 출력
        inorderPrintTree(node.getRight());
    }
     
    // 후위 순회
    public static void postorderPrintTree(Node node) {
        if(node == null)
            return;
         
        // 왼쪽 하위 트리 출력
        postorderPrintTree(node.getLeft());
         
        // 오른쪽 하위 트리 출력
        postorderPrintTree(node.getRight());
         
        // 부모 노드 출력
        System.out.print(" " + node.getData());
    }
}

Test_BinaryTree.java

public class Test_BinaryTree {
    public static void main(String[] args) {
        // 노드 생성
        Node A = new Node('A');
        Node B = new Node('B');
        Node C = new Node('C');
        Node D = new Node('D');
        Node E = new Node('E');
        Node F = new Node('F');
        Node G = new Node('G');
         
        // 트리에 노드 추가
        A.setLeft(B);
        B.setLeft(C);
        B.setRight(D);
         
        A.setRight(E);
        E.setLeft(F);
        E.setRight(G);
         
         
        // 출력
        System.out.println("Preorder...");
        BinaryTree.preorderPrintTree(A);
        System.out.println("\n");
 
        System.out.println("Inorder...");
        BinaryTree.inorderPrintTree(A);
        System.out.println("\n");
         
        System.out.println("Postorder...");
        BinaryTree.postorderPrintTree(A);
    }
}

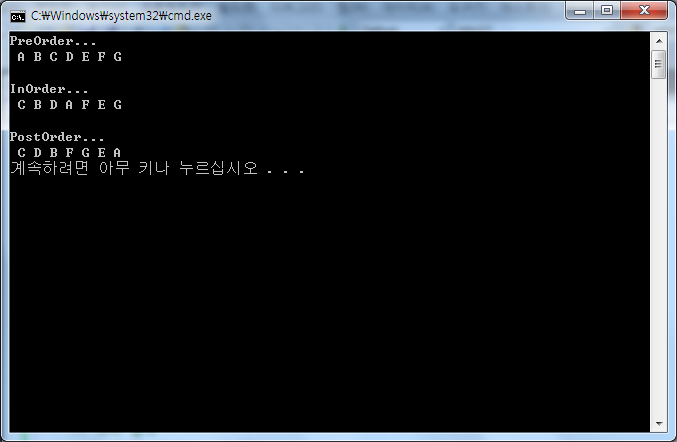
결과)

Preorder...

A B C D E F G

Inorder...

C B D A F E G

Postorder...

C D B F G E A

[출처] http://warmz.tistory.com/619

[c] 이진트리/트리 순회법 코드(전위/중위/후위)

단축키

Articles