Develop
2013.04.23 14:52
베지어 곡선(Bézier curve) 알고리즘(spline 곡선)
조회 수 35506 댓글 3
| 첨부 '6' |
|
|---|
수치해석 분야에서 베지어 곡선은 컴퓨터 그래픽에서 중요한 매개곡선(parametric curve)으로, 이에 대해 수치적으로 안정한 방법은 '드 카스텔죠(de Casteljau)' 알고리즘이다.
베지어 곡선을 더 높은 차원으로 일반화한 것이 베지어 곡면(Bezier surface)이며, 베지어 삼각형(Bezier triangle)은 특수한 경우다.
역사
베지어 곡선은 1959년 'Paul de Casteljau'가 '드 카스텔죠' 알고리즘을 이용해 만들었으며, 1962년 이 곡선을 차체설계에 사용한 프랑스 엔지니어 피에르 베지어(Pierre Bezier)에 의해 널리 알려졌다.
사례 검토
선형 베지어 곡선
점 P0과 P1이 주어지면, 선형 베지어 곡선은 단지 두 점 사이의 직선일 뿐이다. 곡선은 다음으로 주어진다.
2차(Quadratic) 베지어 곡선
2차 베지어 곡선은 함수 B(t), 점 P0, P1, P2를 이용해 그려지는 경로(path)다.
포스트스크립트, 메타폰트, GIMP(GNU Image Manipulation Program) 같은 이미징 시스템은 구부러진 모양을 그리는 데 3차 베지어 곡선으로 만들어진 베지어 스플라인을 사용한다.
일반화
n 단계의 베지어 곡선은 다음처럼 일반화될 수 있다. 점 P0, P1,..., Pn이 주어질 때, 베지어 곡선은
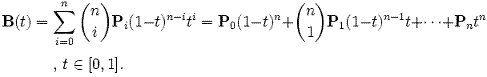
예를 들어, n=5일 때:
용어
몇몇 용어는 다음 매개곡선과 관련이 있다. 다음 식이 있을 때
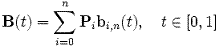
다항식은 다음과 같으며
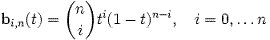
이는 단계 n의 '번스타인 기본 다항식(Bernstein basis polynomials)'으로 알려져있으며, '00 = 1'로 정의되어 있다.
점 Pi는 베지어 곡선의 제어점(control point)이다. 점 P0에서 Pn까지의 베지어 점들(points)을 선으로 연결해서 만들어진 다각형, 즉 Pi의 'convex hull'은 '베지어 다각형'이라 부르며, 베지어 다각형은 베지어 곡선을 포함하고 있다.
주(註)
컴퓨터 그래픽에서의 응용
베지어 곡선은 컴퓨터 그래픽에서 부드러운 곡선을 만드는데 널리 사용된다. 곡선이 제어점의 'convex hull'에 완전히 포함되므로, 그 점들은 시각적으로 보여질 수 있고 직관적으로 곡선을 변경하는데 사용될 수 있다. 이동, 크기변환, 회전 같은 아핀변환(affine transformation)은 곡선의 제어점에 각 변환을 적용함으로써, 곡선에 적용될 수 있다. 가장 중요한 베지어 곡선은 2차와 3차 곡선이다. 더 높은 단계의 곡선은 풀이비용이 비싸다. 더 복잡한 모형이 필요하면, 낮은 차수의 베지어 곡선들(low order Bezier Curves)이 조건(smoothness condition)에 따라 베지어 스플라인 형태로 합쳐진다.
다음 C 코드는 3차 베지어 곡선을 찍는 방법을 보여주는 간단한 예다. 이 예제는 단순히 다항식의 계수를 계산하고 0에서 1까지 변하는 연속적인 t값을 실행한다 − 그래픽 등의 분야에서 종종 '드 카스텔죠'같은 알고리즘이 인용되긴 하지만, 실제 이런 방법을 사용한다. 이는 실제로 이런 선형 알고리즘이 '드 카스텔죠'같은 재귀적인 것보다 더 빠르고 리소스가 덜 소모되기 때문이다. 다음 코드는 명확히하기 위해 인수분해했으며 − 실제로 최적화된 코드는 계수를 한번만 계산하고 곡선 점을 계산하는 실제 루프에서 그 결과를 재사용한다 − 매번 계수를 다시 계산하므로, 덜 효율적이지만 이해는 더 빠를 것이다.
최종 곡선은 곡선 배열에서 연속적인 점들 사이에 선을 그림으로써 그려지게 된다 − 점이 많을수록, 곡선은 더 부드러워진다.
몇몇 아키텍쳐에서는, 아래 코드도 '동적 프로그래밍(dynamic programming)'에 의해 최적화될 수 있다. 가령 dt는 일정하므로, cx * t는 반복때마다 일정 값을 변화시킨다. 이런 최적화를 반복해서 적용함으로써, 루프는 곱셈없이 재작성될 수 있다 (이런 처리는 수치적으로 안정하지는 않다).
/******************************************************
3차(cubic) 베지어 곡선을 만드는 코드 *******************************************************/
typedef struct
{
float x;
float y;
} Point2D;
/******************************************************
cp는 4개의 요소가 있는 배열이다:
cp[0]은 시작점 (A)
cp[1]은 1번째 제어점 (B)
cp[2]는 2번째 제어점 (C)
cp[3]은 끝점 (D) t는 매개변수 값, 0 ≤ t ≤ 1 *******************************************************/
Point2D PointOnCubicBezier( Point2D* cp, float t )
{
float ax, bx, cx;
float ay, by, cy;
float tSquared, tCubed;
Point2D result;
/* 다항식 계수를 계산한다 */
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/* 매개변수 값 t에서 곡선 점을 계산한다 */
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) +
cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) +
cp[0].y;
return result;
}
/*******************************************************
ComputeBezier 함수는 Point2D 구조체 배열을 제어점 cp로부터
만들어진 곡선 점들로 채운다. 호출부는 결과를 저장하기 위한
충분한 메모리를 할당해야하며, 이 크기는
"sizeof(Point2D) * numberOfPoints"
*******************************************************/
void ComputeBezier( Point2D* cp, int numberOfPoints,
Point2D* curve )
{
float dt;
int i;
dt = 1.0 / ( numberOfPoints - 1 );
for( i = 0; i < numberOfPoints; i++)
curve[i] = PointOnCubicBezier( cp, i*dt ); }
베지어 곡선이 쓰이는 또 다른 곳은 애니메이션에서 물체의 운동경로 등이 있다. 여기서 곡선의 x, y 위치는 곡선을 그리는 데 사용되지 않고, 그래픽을 위치시키는 데 사용된다. 이런 방식으로 사용되면, 연속적인 점들 사이의 거리가 중요하게 되는데, 일반적으로 이 점들은 똑같은 간격을 가지지 않는다 − 점들은 제어점들이 서로 가까이 있으면 더 많이 밀집하고, 제어점들이 더 멀리 있으면 넓게 뿌려질 것이다. 선운동 속력(linear motion speed)이 요구된다면, 경로를 따라 결과점들을 고르게 뿌리기 위한 추가 처리가 필요하다.
유리 베지어 곡선(Rational Bézier curves)
원처럼 단순해 보이는 곡선은 베지어 곡선 또는 구간(piecewise) 베지어 곡선으로 표현할 수 없다 (비록 실제로 그 차이는 작고 허용될만한 정도지만). 이런 다른 곡선을 표현하려면, 추가적인 자유도가 필요하다.
유리 베지어 곡선은 적용가능한 가중치를 더한다. 분자는 가중 번스타인 형식 베지어 곡선(weighted Bernstein form Bezier curve)이고 분모는 번스타인 다항식의 가중합(weighted sum)이다.
n+1개의 제어점 Pi가 주어졌을 때, 유리 베지어 곡선은 다음처럼 표현될 수 있으며:
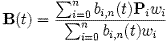
또는 단순히 다음처럼 표현할 수도 있다
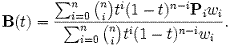
참조
드 카스텔죠 알고리즘
스플라인 (수학)
베지어 스플라인
베지어 곡면(surface)
베지어 삼각형
NURBS(Non-Uniform Rational B-Spline)
참고문헌
Paul Bourke: Bézier curves, http://astronomy.swin.edu.au/~pbourke/curves/bezier/
Donald Knuth: Metafont: the Program, Addison-Wesley 1986, pp. 123-131. 구현 세부사항에 대한 훌륭한 문서; TeX 배포의 일부로 무료.
Dr. Thomas Sederberg, BYU Bézier curves,http://www.tsplines.com/resources/class_notes/Bezier_curves.pdf
외부링크
Bezier Curves interactive appliet
3rd order Bezier Curves applet
Living Math Bézier applet
Living Math Bézier applets of different spline types, JAVA programming of splines inAn Interactive Introduction to Splines
Don Lancaster's Cubic Spline Library는 이미지 보간(image interpolation)을 위한 3차 스플라인을 사용해, 베지어 곡선으로 원 (또는 원호나 쌍곡선) 을 근사하는 방법과 수학적 배경을 설명한다.
베지어 곡선을 더 높은 차원으로 일반화한 것이 베지어 곡면(Bezier surface)이며, 베지어 삼각형(Bezier triangle)은 특수한 경우다.
내용
1. 역사
2. 사례 검토
2.1 선형 베지어 곡선
2.2 2차 베지어 곡선
2.3 3차 베지어 곡선
3. 일반화
3.1 용어
3.2 주(註)
4. 컴퓨터 그래픽에서의 응용
5. 유리 베지어 곡선
6. 참조
7. 참고문헌
8. 외부링크
1. 역사
2. 사례 검토
2.1 선형 베지어 곡선
2.2 2차 베지어 곡선
2.3 3차 베지어 곡선
3. 일반화
3.1 용어
3.2 주(註)
4. 컴퓨터 그래픽에서의 응용
5. 유리 베지어 곡선
6. 참조
7. 참고문헌
8. 외부링크
역사
베지어 곡선은 1959년 'Paul de Casteljau'가 '드 카스텔죠' 알고리즘을 이용해 만들었으며, 1962년 이 곡선을 차체설계에 사용한 프랑스 엔지니어 피에르 베지어(Pierre Bezier)에 의해 널리 알려졌다.
사례 검토
선형 베지어 곡선
점 P0과 P1이 주어지면, 선형 베지어 곡선은 단지 두 점 사이의 직선일 뿐이다. 곡선은 다음으로 주어진다.
B(t) = (1−t)P0+tP1, t∈[0,1]
2차(Quadratic) 베지어 곡선
2차 베지어 곡선은 함수 B(t), 점 P0, P1, P2를 이용해 그려지는 경로(path)다.
B(t) = (1−t)2P0+2t(1−t)P1+t2P2, t∈[0,1]
트루타입 글꼴은 2차 베지어 곡선으로 만들어진 베지어 스플라인(spline)을 사용한다.
3차(Cubic) 베지어 곡선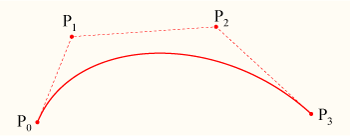
평면 또는 3차원 공간에서 4개의 점 P0, P1, P2, P3은 3차 베지어 곡선을 정의한다. 곡선은 P0을 출발해P1, P2 방향으로 향한 후 P3에 도착한다. 일반적으로 P1이나 P2는 거치지않으며, 방향정보를 제공하기위해 존재한다. P0와 P1 사이의 거리는 P3로 돌아서기 전, P2와 곡선 간의 거리를 결정한다.
곡선의 매개형식은 다음과 같다:
B(t) = P0(1−t)3+3P1t(1−t)2+3P2t2(1−t)+P3t3, t∈[0,1]
포스트스크립트, 메타폰트, GIMP(GNU Image Manipulation Program) 같은 이미징 시스템은 구부러진 모양을 그리는 데 3차 베지어 곡선으로 만들어진 베지어 스플라인을 사용한다.
일반화
n 단계의 베지어 곡선은 다음처럼 일반화될 수 있다. 점 P0, P1,..., Pn이 주어질 때, 베지어 곡선은
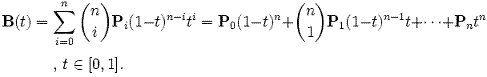
예를 들어, n=5일 때:
B(t) =P0(1−t)5+5P1t(1−t)4+10P2t2(1−t)3+10P3t3(1−t)2+5P4t4(1−t)+P5t5,t∈[0,1]
용어
몇몇 용어는 다음 매개곡선과 관련이 있다. 다음 식이 있을 때
다항식은 다음과 같으며
이는 단계 n의 '번스타인 기본 다항식(Bernstein basis polynomials)'으로 알려져있으며, '00 = 1'로 정의되어 있다.
점 Pi는 베지어 곡선의 제어점(control point)이다. 점 P0에서 Pn까지의 베지어 점들(points)을 선으로 연결해서 만들어진 다각형, 즉 Pi의 'convex hull'은 '베지어 다각형'이라 부르며, 베지어 다각형은 베지어 곡선을 포함하고 있다.
주(註)
- 곡선은 P0에서 시작해서 Pn에서 끝난다; 이것이 이른바 '종점 보간(endpoint interpolation)' 속성이다.
- 모든 제어점이 곡선상에 있으면 직선이며, 비슷하게, 제어점들이 동일선상에 있으면 베지어 곡선은 직선이다. (즉, 곡선이 직선이기 위한 필요충분조건은 모든 제어점이 곡선상에 있는 것이며, 베지어 곡선이 직선이기 위한 필요충분조건은 제어점들이 동일선상에 있는 것이다)
- 곡선의 시작 (끝) 은 베지어 다각형의 처음 (마지막) 섹션에 접한다.
- 곡선은 어떤 점에서라도 2개 이상의 곡선으로 나누어질 수 있으며, 나누어진 각각의 곡선 또한 베지어 곡선이다.
- 베지어 곡선으로는 원 뿐 아니라 원호조차도 정확히 그릴 수 없다. 하지만, 종종 베지어 곡선은 충분히 작은 원호에 대한 적절한 근사치를 제공한다.
- 베지어 곡선에서 일정 거리만큼 떨어져 있는 "평행한" 곡선은 몇몇 사소한 경우를 제외하고 정확한 베지어 곡선이 될 수 없다. 하지만, 실제 목적에 맞게 적절한 근사치를 제공하는 '발견법(heuristic method)'은 있다.
컴퓨터 그래픽에서의 응용
베지어 곡선은 컴퓨터 그래픽에서 부드러운 곡선을 만드는데 널리 사용된다. 곡선이 제어점의 'convex hull'에 완전히 포함되므로, 그 점들은 시각적으로 보여질 수 있고 직관적으로 곡선을 변경하는데 사용될 수 있다. 이동, 크기변환, 회전 같은 아핀변환(affine transformation)은 곡선의 제어점에 각 변환을 적용함으로써, 곡선에 적용될 수 있다. 가장 중요한 베지어 곡선은 2차와 3차 곡선이다. 더 높은 단계의 곡선은 풀이비용이 비싸다. 더 복잡한 모형이 필요하면, 낮은 차수의 베지어 곡선들(low order Bezier Curves)이 조건(smoothness condition)에 따라 베지어 스플라인 형태로 합쳐진다.
다음 C 코드는 3차 베지어 곡선을 찍는 방법을 보여주는 간단한 예다. 이 예제는 단순히 다항식의 계수를 계산하고 0에서 1까지 변하는 연속적인 t값을 실행한다 − 그래픽 등의 분야에서 종종 '드 카스텔죠'같은 알고리즘이 인용되긴 하지만, 실제 이런 방법을 사용한다. 이는 실제로 이런 선형 알고리즘이 '드 카스텔죠'같은 재귀적인 것보다 더 빠르고 리소스가 덜 소모되기 때문이다. 다음 코드는 명확히하기 위해 인수분해했으며 − 실제로 최적화된 코드는 계수를 한번만 계산하고 곡선 점을 계산하는 실제 루프에서 그 결과를 재사용한다 − 매번 계수를 다시 계산하므로, 덜 효율적이지만 이해는 더 빠를 것이다.
최종 곡선은 곡선 배열에서 연속적인 점들 사이에 선을 그림으로써 그려지게 된다 − 점이 많을수록, 곡선은 더 부드러워진다.
몇몇 아키텍쳐에서는, 아래 코드도 '동적 프로그래밍(dynamic programming)'에 의해 최적화될 수 있다. 가령 dt는 일정하므로, cx * t는 반복때마다 일정 값을 변화시킨다. 이런 최적화를 반복해서 적용함으로써, 루프는 곱셈없이 재작성될 수 있다 (이런 처리는 수치적으로 안정하지는 않다).
/******************************************************
3차(cubic) 베지어 곡선을 만드는 코드 *******************************************************/
typedef struct
{
float x;
float y;
} Point2D;
/******************************************************
cp는 4개의 요소가 있는 배열이다:
cp[0]은 시작점 (A)
cp[1]은 1번째 제어점 (B)
cp[2]는 2번째 제어점 (C)
cp[3]은 끝점 (D) t는 매개변수 값, 0 ≤ t ≤ 1 *******************************************************/
Point2D PointOnCubicBezier( Point2D* cp, float t )
{
float ax, bx, cx;
float ay, by, cy;
float tSquared, tCubed;
Point2D result;
/* 다항식 계수를 계산한다 */
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/* 매개변수 값 t에서 곡선 점을 계산한다 */
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) +
cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) +
cp[0].y;
return result;
}
/*******************************************************
ComputeBezier 함수는 Point2D 구조체 배열을 제어점 cp로부터
만들어진 곡선 점들로 채운다. 호출부는 결과를 저장하기 위한
충분한 메모리를 할당해야하며, 이 크기는
"sizeof(Point2D) * numberOfPoints"
*******************************************************/
void ComputeBezier( Point2D* cp, int numberOfPoints,
Point2D* curve )
{
float dt;
int i;
dt = 1.0 / ( numberOfPoints - 1 );
for( i = 0; i < numberOfPoints; i++)
curve[i] = PointOnCubicBezier( cp, i*dt ); }
베지어 곡선이 쓰이는 또 다른 곳은 애니메이션에서 물체의 운동경로 등이 있다. 여기서 곡선의 x, y 위치는 곡선을 그리는 데 사용되지 않고, 그래픽을 위치시키는 데 사용된다. 이런 방식으로 사용되면, 연속적인 점들 사이의 거리가 중요하게 되는데, 일반적으로 이 점들은 똑같은 간격을 가지지 않는다 − 점들은 제어점들이 서로 가까이 있으면 더 많이 밀집하고, 제어점들이 더 멀리 있으면 넓게 뿌려질 것이다. 선운동 속력(linear motion speed)이 요구된다면, 경로를 따라 결과점들을 고르게 뿌리기 위한 추가 처리가 필요하다.
유리 베지어 곡선(Rational Bézier curves)
원처럼 단순해 보이는 곡선은 베지어 곡선 또는 구간(piecewise) 베지어 곡선으로 표현할 수 없다 (비록 실제로 그 차이는 작고 허용될만한 정도지만). 이런 다른 곡선을 표현하려면, 추가적인 자유도가 필요하다.
유리 베지어 곡선은 적용가능한 가중치를 더한다. 분자는 가중 번스타인 형식 베지어 곡선(weighted Bernstein form Bezier curve)이고 분모는 번스타인 다항식의 가중합(weighted sum)이다.
n+1개의 제어점 Pi가 주어졌을 때, 유리 베지어 곡선은 다음처럼 표현될 수 있으며:
또는 단순히 다음처럼 표현할 수도 있다
참조
참고문헌
외부링크
| 번호 | 분류 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|---|
| 757 | Develop |
[c] 공용체를 이용해 MSB를 LSB로 변환
|
hooni | 2013.04.23 | 10330 |
| 756 | Develop |
[c] 함수 목록과 예제 소스 파일
|
hooni | 2013.04.23 | 8814 |
| 755 | Develop |
[c] 윈도우 API Viewport와 Window
|
hooni | 2013.04.23 | 8583 |
| 754 | Develop |
[c] 윈도우 API sin 함수 출력..
|
hooni | 2013.04.23 | 16631 |
| » | Develop |
베지어 곡선(Bézier curve) 알고리즘(spline 곡선)
3 |
hooni | 2013.04.23 | 35506 |
| 752 | Develop |
[c] 압축 알고리즘 소스 및 정리
|
hooni | 2013.04.23 | 9937 |
| 751 | Develop |
[c] 구구단 최단라인 ㅡㅡ;
|
hooni | 2013.04.23 | 9357 |
| 750 | System/OS | [ms-sql] 서브스트링(substring), 프로시저(SP) 작성 예제 | hooni | 2013.04.23 | 42694 |
| 749 | Develop |
[c++] 초간단 스택 두 가지 방식(class, struct)
|
hooni | 2013.04.23 | 8898 |
| 748 | Develop |
[c][java] 주사선 채우기 알고리즘(scan line filling algorithm) 구현
|
hooni | 2013.04.23 | 10256 |
| 747 | Develop |
[c] 더블(이중) 연결리스트 예제..
|
hooni | 2013.04.23 | 8838 |
| 746 | Develop |
[c++] 헤더, 소스 파일 분리해서 작성해본 테스트 소스
|
hooni | 2013.04.23 | 7942 |
 [c] 윈도우 API sin 함수 출력..
[c] 윈도우 API sin 함수 출력..

http://picomax.net/xe/index.php?mid=study&document_srl=4120